Home  ›  Problem 1 for the Plane Area Below Colored in Light Blue Locate the Centroid

Problem 1 for the Plane Area Below Colored in Light Blue Locate the Centroid

Written By Tuesday, July 5, 2022 Add Comment Edit

17.3: Centroids in Volumes and Center of Mass via Integration

  1. Last updated
  2. Save as PDF
  • Page ID
    55340

    • The centroid of a volume can be thought of as the geometric center of that shape. It is often denoted as \(C\), being being located at the coordinates \((\bar{x}, \bar{y}, \bar{z})\). If this volume represents a part with a uniform density (like most single material parts) then the centroid will also be the center of mass, a point usually labeled as \(G\).

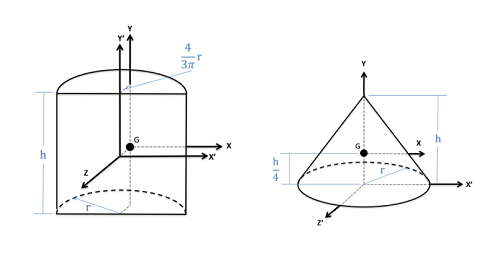
    A half-cylinder of height h, extruded from a semicircle of radius r, has its centroid located along the line of intersection of its two planes of symmetry, 4r/(3 pi) units away from the midpoint of the semicircle's straight edge. A right circular cone of radius r and height h, standing on its base, has its centroid located h/4 units above the midpoint of its base.
    Figure \(\PageIndex{1}\): The centroid point (\(C\)) or the center of mass (\(G\)) for some common shapes. (The centroid and center of mass are the same point for bodies with a uniform density)

    Just as with the centroids of an area, centroids of volumes and the center of mass are useful for a number of situations in the mechanics course sequence, including the analysis of distributed forces, simplifying the analysis of gravity (which is itself a distributed force), and as an intermediate step in determining mass moments of inertia.

    Just as with areas, the location of the centroid (or center of mass) for a variety of common shapes can simply be looked up in tables, such as this one. However, we will often need to determine the centroid or center of mass for other shapes, and to do this we will generally use one of two methods.

    1. We can use the first moment integral to determine the centroid or center of mass location.
    2. We can use the method of composite parts along with centroid tables to determine the centroid or center of mass location.

    On this page we will only discuss the first method, as the method of composite parts is discussed in a later section. However, the tables used in the method of composite parts are derived via the first moment integral, so both methods ultimately rely on first moment integrals.

    Finding the Centroid of a Volume via the First Moment Integral

    When we find the centroid of a three-dimensional shape, we will be looking for the \(x\), \(y\), and \(z\) coordinates (\(\bar{x}\), \(\bar{y}\), and \(\bar{z}\)) of the point that is the centroid of the shape.

    Much like the centroid calculations we did with two-dimensional shapes, we are looking to find the shape's average coordinate in each dimension. We do this by summing up all the little bits of volume times the \(x\), \(y\), or \(z\) coordinate of that bit of volume and then dividing that sum by the total volume of the shape. Again we will use calculus to sum up an infinite number of infinitely small volumes. Specifically this sum will be the first rectangular volume moment integral for the shape.

    \[ C = G = (\bar{x}, \bar{y}, \bar{z}) \quad \text{for constant-density shapes} \nonumber\]

    Working in each of the three coordinate directions we wind up with the following three equations.

    \[\begin{align*} \bar{x} &= \dfrac{\displaystyle \int_V (dV * x)}{V} \\[4pt] \bar{y} &= \dfrac{\displaystyle \int_V (dV * y)}{V} \\[4pt] \bar{z} &= \dfrac{\displaystyle \int_V (dV * z)}{V} \end{align*}\]

    With these new equations we have the variable \(dV\) rather than \(dA\), because we are integrating over a volume rather than an area. This represents the rate of change of the volume as we move along an axis from one end to another. The rate of change of the volume at any point on the shape will be the cross-sectional area that is perpendicular to that axis times the rate at which we are moving along that axis. Since cross-sectional area may vary as we move along the axis, we will need to determine a formula for the cross sectional area at any point along that axis.

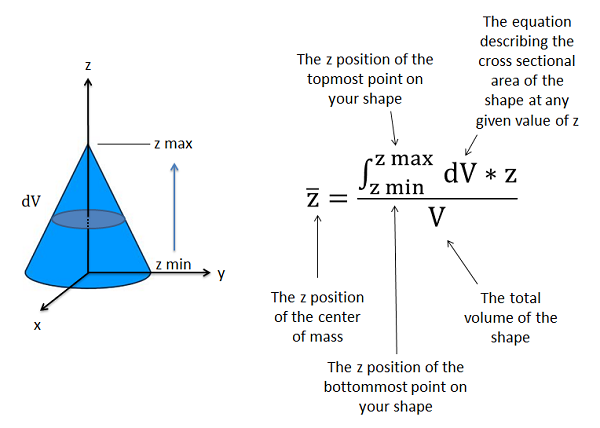
    A right circular cone lies with its base on the xy-plane, centered at the origin, and its tip at some point on the positive z-axis. The tip's z-coordinate is labeled z_max, and the xy-plane (z=0) is labeled z_min. The cone is sliced parallel to the xy-plane into thin circular slices, each with a volume dV equaling the cross-sectional area times the small change in z that represents the slice height. The equation for the z-coordinate of the cone's centroid is the integral of dV times z, evaluated from x_min to x_max, the whole divided by the cone's total volume.
    Figure \(\PageIndex{2}\): The \(z\)-coordinate of the centroid/center of mass.

    Using the first moment integral and the equations shown above, we can theoretically find the centroid of any volume as long as we can write an equation to describe the cross section area for each direction. For more complex shapes, however, determining these equations and then integrating these equations may become very time-consuming. For these complex shapes, the method of composite parts or computer tools will most likely be much faster.

    Using Symmetry as a Shortcut

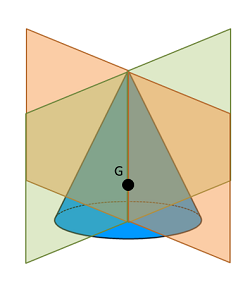
    Just as with 2D areas, shape symmetry can provide a shortcut in many centroid calculations. Remember that the centroid coordinate is the average \(x\), \(y\), and \(z\) coordinate for all the points in the shape. If the volume has a plane of symmetry, that means each point on one side of the line must have an equivalent point on the other side of the line. This means that the average value (AKA the centroid) must lie within that plane. If the volume has more than one plane of symmetry, then the centroid must exist at the intersection of those planes.

    A right circular cone has many planes of symmetry, all passing through the line connecting the tip to the center of the circular base. Therefore, the centroid is somewhere located along that line.
    Figure \(\PageIndex{3}\): If a volume has a plane of symmetry, then the centroid must lie somewhere in that plane. If the volume has more than one plane of symmetry, the centroid must exist at the intersection of those planes.

    Finding the Center of Mass for Non-Uniform Density Shapes

    If a body has a non-uniform density, then the centroid of the volume and the center of mass will no longer be the same point. In these cases, we will be integrating with respect to mass, rather than integrating the volume. To do this, we will use something called a density function, which will provide the density (the mass per unit volume) in terms of the \(x\), \(y\), and/or \(z\) location. In the end, we will also be dividing by total mass, rather than dividing by total volume. The generalized equations for the center of mass are shown in the equations below.

    \[ C \neq G \]

    \[ G = (x_G, y_G, z_G) \]

    \begin{align} x_G &= \dfrac{\int_m (dm*x)}{m} = \dfrac{\int_V (\rho (x,y,z) * dV * x)}{m} \\[4pt] y_G &= \dfrac{\int_m (dm*y)}{m} = \dfrac{\int_V (\rho (x,y,z) * dV * y)}{m} \\[4pt] z_G &= \dfrac{\int_m (dm*z)}{m} = \dfrac{\int_V (\rho (x,y,z) * dV * z)}{m} \end{align}

    In instances of uniform density (where the density function did not vary with location and was therefore just a constant), the density constant could be moved outside of the integral. On the bottom, we could also write mass as density times volume, and the density terms on the top and bottom of the fraction would cancel out. That is why for uniform-density parts, the centroid and center of mass will be the same point.

    When we have a density function that is not a constant, we will have to come up with a mathematical function for the density in terms of \(x\) and/or \(y\) and/or \(z\) locations. If density varies along more than one axis, determining the function and then integrating it may become quite difficult, and computer modeling may be advisable in these situations.

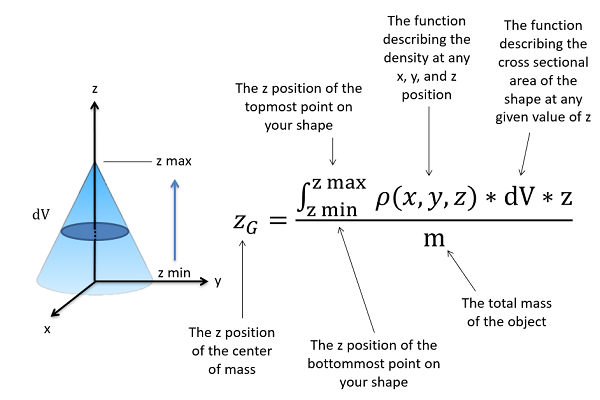
    A right circular cone lies with its base on the xy-plane, centered at the origin, and its tip at some point on the positive z-axis. The tip's z-coordinate is labeled z_max, and the xy-plane (z=0) is labeled z_min. The cone is sliced parallel to the xy-plane into thin circular slices, each with a volume dV equaling the cross-sectional area times the small change in z that represents the slice height. The equation for the z-coordinate of the cone's center of mass is the integral of the density function times dV times z, evaluated from x_min to x_max, the whole divided by the cone's total mass.
    Figure \(\PageIndex{4}\): To find the center of mass of a body with a continuously varying density, we must have an equation to describe the density based on position.

    Once you have the density function, you will multiply that by the relevant \(dV\) function as discussed earlier on the page and multiply it by the variable for the relevant axis. This entire function is integrated from left to right, bottom to top, or back to front, and then that quantity is divided by mass to find the location of the center of mass.

    Video lecture covering this section, delivered by Dr. Jacob Moore. YouTube source: https://youtu.be/cBiWKfBLEhk.

    Example \(\PageIndex{1}\)

    The cone shown below is four inches tall and has a four-inch-diameter base. Find the \(x\), \(y\), and \(z\) coordinates of the centroid.

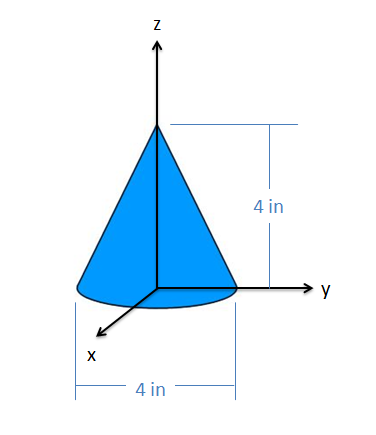
    A right circular cone with radius 2 inches has its base located on the xy-plane, centered at the origin. Its tip is located on the z-axis, 4 inches above the base.
    Figure \(\PageIndex{5}\): problem diagram for Example \(\PageIndex{1}\). A cone has a circular base centered on the \(xy\)-plane of a Cartesian coordinate system, and a central axis that stretches along the positive \(z\)-axis.
    Solution:
    Video \(\PageIndex{2}\): Worked solution to example problem \(\PageIndex{1}\), provided by Dr. Jacob Moore. YouTube source: https://youtu.be/IJHwNaOG4-s.

    Example \(\PageIndex{2}\)

    Find the y coordinate of the centroid for the tetrahedron shown in the image below. (The fourth vertex is at the origin)

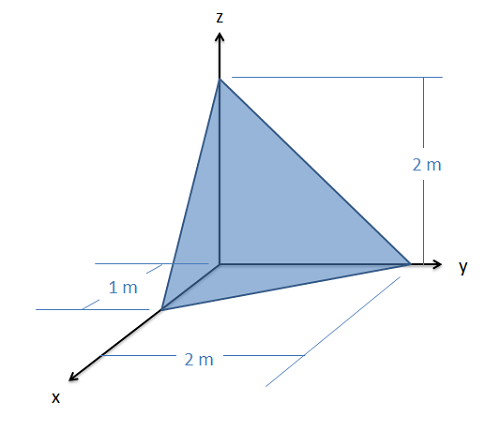
    A tetrahedron in the first octant of a Cartesian coordinate system has vertexes located at the points (0, 0, 0), (1, 0, 0), (0, 2, 0), and (0, 0, 2). All units are in meters.
    Figure \(\PageIndex{6}\): problem diagram for Example \(\PageIndex{2}\). A tetrahedron lies in the first octant of a Cartesian coordinate system, with three of its edges formed by the coordinate axes.
    Solution:
    Video \(\PageIndex{3}\): Worked solution to example problem \(\PageIndex{2}\), provided by Dr. Jacob Moore. YouTube source: https://youtu.be/itu_P4ysw9g.

    Example \(\PageIndex{3}\)

    A water and ceramic slurry with a uniform density of 1100 kilograms per meter cubed enters a settling tank with a height of 1 meter and a diameter of 1 meter. After one hour in the tank, the density of the slurry at the top of the tank is measured to be 1000 kilograms per meter cubed and the density at the bottom of the tank is measured to be 1200 kilograms per meter cubed. Assume the density of the slurry varies linearly between the top and the bottom. How far has the center of mass of the slurry dropped between the initial conditions and the current state?

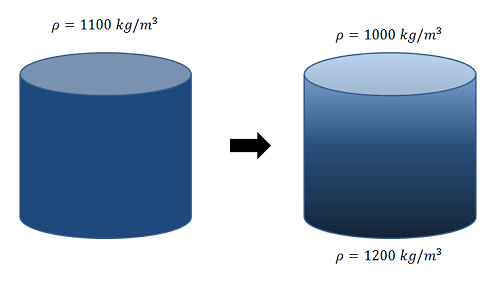
    A cylinder on the left is uniformly colored a medium blue, and has a uniform density of 1100 kg/m³. An identically sized cylinder on the right represents the tank after 1 hour; this cylinder's color is a steady gradient of light blue at the top to dark blue at the bottom. The density of the top of this tank is 1000 kg/m³, and the density of the bottom is 1200 kg/m³.
    Figure \(\PageIndex{7}\): problem diagram for Example \(\PageIndex{3}\). As particles in a tank settle, a solution of originally uniform density becomes one with linearly decreasing density from bottom to top.
    Solution:
    Video \(\PageIndex{4}\): Worked solution to example problem \(\PageIndex{3}\), provided by Dr. Jacob Moore. YouTube source: https://youtu.be/BTyO2HolIHY.

    timberlakehuned2001.blogspot.com

    Source: https://eng.libretexts.org/Bookshelves/Mechanical_Engineering/Mechanics_Map_(Moore_et_al.)/17%3A_Appendix_2_-_Moment_Integrals/17.3%3A_Centroids_in_Volumes_and_Center_of_Mass_via_Integration

    0 Response to "Problem 1 for the Plane Area Below Colored in Light Blue Locate the Centroid"

    Post a Comment

    Subscribe to: Post Comments (Atom)

    Iklan Atas Artikel

    Iklan Tengah Artikel 1

    Iklan Tengah Artikel 2

    Iklan Bawah Artikel